无偿征集连续性随机变量期望题的答案
kalmanfans
posted @ 2012年2月18日 09:58
in 在德意志插队的日子
with tags
斯图加特 stuttgart airport
, 2137 阅读
问题描述：
生命中总有不经意的地方，她改变了你命运的轨迹， it will change your life training plan, in a uncontemplated way!
斯图加特飞机场离斯图加特市中心很近，并且位于其市内交通（S-Bahn）网络内。其中，有两条线经过斯图加特飞机场站Flughafen：S2,S3. S2 和S3都是每隔半小时一班，二者之间有一个固定的时间间隔T（斯图的情况是T=10分钟）。
现在的问题是：
假设小八路从飞机场以随机的概率走到S bahn Flughafen站台，她平均要等多久，才能坐上S Bahn线回家？
固定的时间T会对这个期望值有影响吗？
答案形式：
先提供最终答案，如果答案正确，Kalmanfans将联系你，要求提供求证过程。
截止日期：2013.01.04
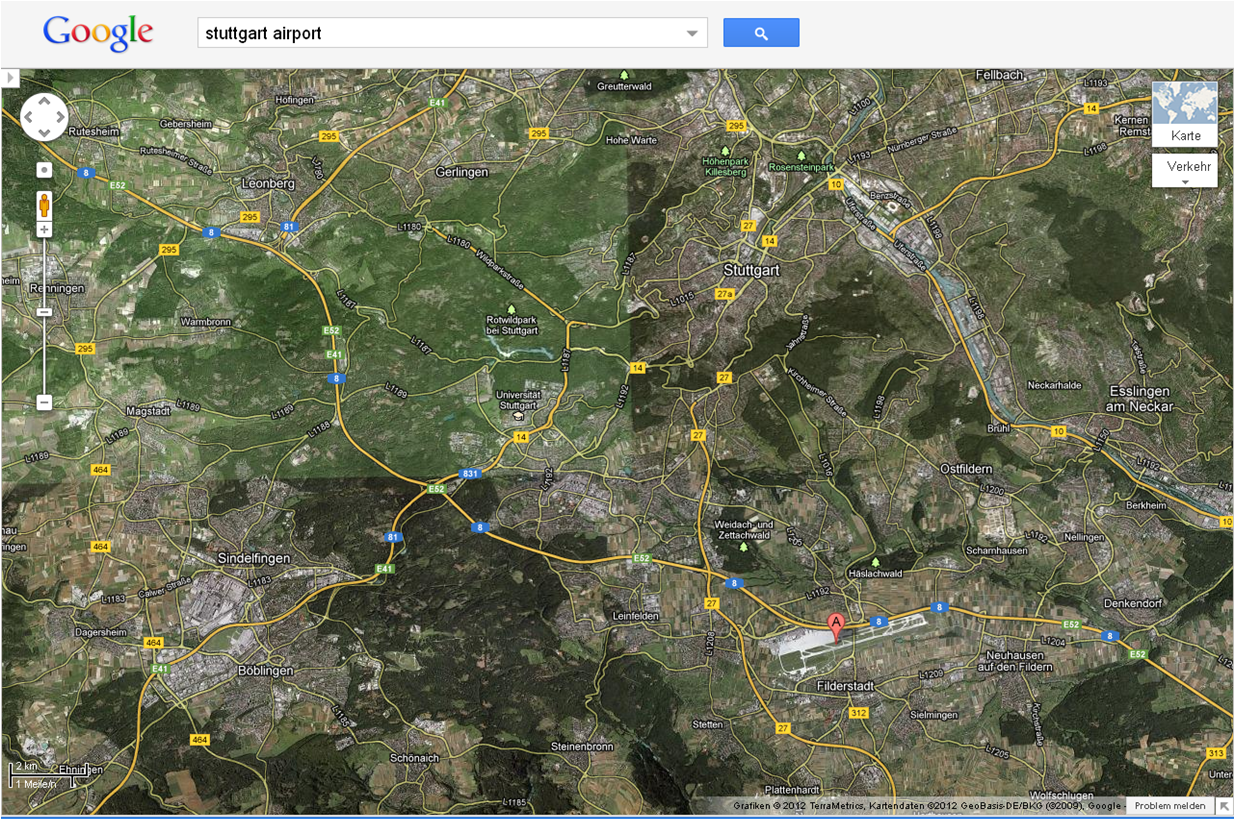
(点击此图可放大)图中的A点，就是斯图飞机场，也是我的A点。
无论多久，我要等你！
kalmanfans
搜索
日历
| 十一月 | ||||||
|---|---|---|---|---|---|---|
| 日 | 一 | 二 | 三 | 四 | 五 | 六 |
| 27 | 28 | 29 | 30 | 31 | 1 | 2 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
分类
- ArcGIS
- Matlab
- Fortan
- Software application
- 爱你爱家
- Data Visualization
- Telematics Transport
- Kalman Filter, Monte Carlo, ANN
- Network Analysis
- Location Based Service LBS
- Office TOY & Funing Puzzle
- Mathematical Modeling
- 建筑 规划 设计
- 在德意志插队的日子
- Culture Philosophy
- ways to research
- 电影 音乐
- 每周一则新闻
- Bernese
- Quantum mechanics
- 数据库
最新评论
最新留言
链接
RSS
2012年2月19日 08:21
最可怕的事情，你发现比你牛的人比你还努力！
2012年8月22日 14:44
假设S2和S3的固定间隔是T1， S2和S3本身的间隔T2， T2 > T1, 期望是
(T1^2 + (T2-T1)^2)/(2*T2), 上限T2/2(T1 = 0)， 下限T2/4(T1 = T2/2), 期望大小与T1有关
你目前的设定下8.3分钟
2014年2月10日 12:56
The tact of s2 s3 are both Tx=30min,
then the small gap betwenn s2 and s3 is T1, as ur assumption T1=10min, the bigger gap is T2=Tx-T1=20min
Assume Passenger arrive at time Tk,
case 1: Tk lies in small gap T1, waiting time X is uniformly distributied
X1~U(0,10), E(X1)=(10-0)/2=5
the probability of Case 1 is P1=1/3
similarly Case 2: X2~U(0,20) E(X2)=(20-0)/2=10
P2=2/3
E(Xtotal)=P1*E(X1)+P2*E(X2)=25/3 Min